odd function integral|examples of odd functions : iloilo An odd function is one in which f( − x) = − f(x) for all x in the domain, and the graph of the function is symmetric about the origin. Integrals of even functions, when the limits of . How about that one of the first games to feature modern first-person-shooter controls was Alien Resurrection on the original Playstation? Or how about the fact that every 3D game Nintendo has ever made, can trace its roots back to a Game Boy demo developed by a teenager in the UK? . Especially in that era of video games a lot of .
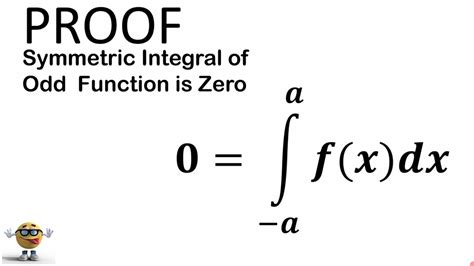
odd function integral,An odd function is one in which f (−x)= −f (x) f ( − x) = − f ( x) for all x x in the domain, and the graph of the function is symmetric about the origin. Integrals of even functions, when the limits of integration are from − a a to a a, involve two equal areas, because they are .
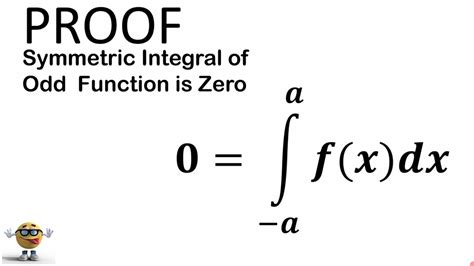
Definite integrals of even and odd functions. What to do if you think the function is even or odd. Sometimes we can simplify a definite integral if we recognize .Learn how to find integrals of even and odd functions on symmetric intervals using properties and special methods. See examples, solutions, and tips for evaluating .An odd function is one in which f( − x) = − f(x) for all x in the domain, and the graph of the function is symmetric about the origin. Integrals of even functions, when the limits of . Let f be an odd function with a primitive on the open interval ( − a.. a), where a > 0 . Then the improper integral of f on ( − a.. a) is: ∫ → a → − af(x)dx = 0.
For an odd function, I know that f(x) = - f(x). I'm trying to show that $\int^{a}_{-a} f(x) dx$ = 0. I've seen the proof where it splits the integral up into: . If the range of the definite integral is -a to a, and if the function is odd, then the value of the integral is 0. To determine if the function is odd, plug -x in for x, and then simplify. If. Example 1.2.11 Odd functions. Three examples of odd functions are \(f(x)=\sin x\text{,}\) \(f(x)=\tan x\) and \(f(x)=x^3\text{.}\) In fact, if \(f(x)\) is any odd power .If the graph of y = f(x) is symmetric with respect to the y-axis, then we call f an even function. Similarly, if the graph of y = f(x) is symmetric with the respect to the origin, .
Symmetry appears throughout mathematics in many different forms, and its use often leads to insights and efficiencies. Here we use the symmetry of a function to simplify integral calculations. Section 1.1 introduced . Theorem 1.2.1 Arithmetic of Integration. Let a, b and A, B, C be real numbers. Let the functions f(x) and g(x) be integrable on an interval that contains a and b. Then. (a) ∫b a(f(x) + g(x))dx = ∫b af(x)dx + ∫b ag(x)dx (b) ∫b a(f(x) − g(x))dx = ∫b af(x)dx − ∫b ag(x)dx (c) ∫b aCf(x)dx = C ⋅ ∫b af(x)dx. Combining these three .The product of any two odd functions is an even function. The quotient of any 2 odd functions is an even function. Composition: The composition of any 2 odd functions is odd. The derivative of any given odd function is even in nature. The integral of any given odd function from the limits – A to + A is 0.odd function integral examples of odd functions2. Start by splitting the integral into two pieces, the part over negatives values of x and the part over positive values. ∫2 − 2f(x)dx = ∫0 − 2f(x)dx + ∫2 0f(x)dx. From here you can apply the definition of an even or odd function. Cite. answered Feb 13, .
They are special types of functions. Even Functions. A function is "even" when: f(x) = f(−x) for all x In other words there is symmetry about the y-axis (like a reflection):. This is the curve f(x) = x 2 +1. They are called "even" functions because the functions x 2, x 4, x 6, x 8, etc behave like that, but there are other functions that behave like that too, such as .
odd function integral 4. Often in mathematics, particularly in physics, we welcome definite integrals from −∞ − ∞ to ∞ ∞ of odd functions, since they are equal to zero. Such as. ∫∞ −∞ sin(x)dx = 0 ∫ − ∞ ∞ sin. . ( x) d x = 0 . So, simple question; why does WolframAlpha fail to evaluate infinite bounded definite integrals of odd .3. It might be nit picking but your proof should be as follows: Assume f is odd. First observe. ∫a −a f(x) dx = ∫a 0 f(x) dx +∫0 −a f(x) dx. Using x = −u substitution in the second integral yields. ∫0 −a f(x) dx = −∫0 a f(−u) du =∫a 0 f(−u) du. And since f is odd, then it follows. ∫a 0 f(−u) du = −∫a 0 f(u) du.examples of odd functions Even and Odd Functions. During the course of our study of integrals of functions of one variable, we found that the evaluation of certain integrals could be substantially simplified by exploiting symmetry properties of the integrand. Concretely, in Section 1.2.1 of the CLP-2 text, we gave the
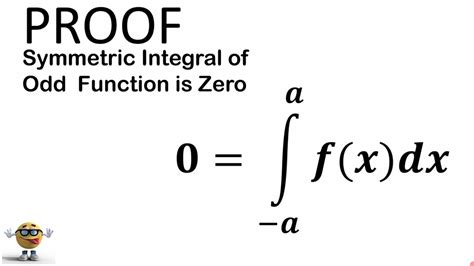
The theorem of “Integration of Even and Odd Functions” is a way to find integrals for odd and even functions. It’s a method that makes some challenging definite integrals easier to find. In order to use it, you have to be evaluating a function over an interval that’s either symmetric about the origin or symmetric about the y-axis [1].
odd function integral|examples of odd functions
PH0 · integral calculus definition
PH1 · integral calculus
PH2 · examples of odd functions
PH3 · even function integral property
PH4 · difficult integral problems
PH5 · Iba pa